Dark matter halos are the building blocks of the cosmic structure formation. They are gravitationally bound concentrations of dark matter particles in which cooling baryonic gas falls in to form the stars and galaxies that we observe today. The largest halos in the universe host massive cluster of galaxies (M 1015 Msun), while the smallest ones may host dwarf galaxies (M 108 Msun) forming a population of satellites swirling around galaxies such as the Milky Way. Their mass range spans several orders of magnitudes. How likely are these objects to exist? How are they spatially distributed? Do their properties change over time? Over the past decade cosmologists have tackled this challenge by running large N-body simulations on the most powerful supercomputers to solve the complexity of the non-linear gravitational interactions involved in the formation of dark matter halos (Figure 1). Nevertheless a complete theoretical understanding of the properties of the halo mass distribution has been missing.

A mathematical description of individual halos emerging from the spatial distribution of tiny density fluctuations is too hard a problem to solve. In the end, one is only interested in determining the average properties of the halo mass distribution, since these can be directly confronted with measurements of the observed abundance of massive clusters. And this is a much more accomplishable task. Pier Stefano Corasaniti, theoretical cosmologist at LUTH, and Ixandra Achitouv, PhD student at the University of Paris VII, have performed the first ab initio calculation reproducing with unprecedented accuracy the halo mass distribution measured in N-body simulations. To achieve this result, they have worked out a stochastic model of the halo formation process. The idea is to extrapolate the properties of the halo mass distribution from the statistics of initial density field which is accurately measured from observations of Cosmic Microwave Background anisotropies. This inference is realized by filtering the primordial density field over different length scales, with the filter function defining volumes of space to which correspond different halo masses. The formation of halos is then assimilated to random walks of the density fluctuation as function of the filtering radius playing the role of pseudo-time variable. A halo is formed when a random walk hits a characteristic density threshold of collapse (Figure 2). The determination of the halo mass distribution is then reduced to simply counting the fraction of random walks that cross such a threshold as function of the filter scale (or the associated mass).
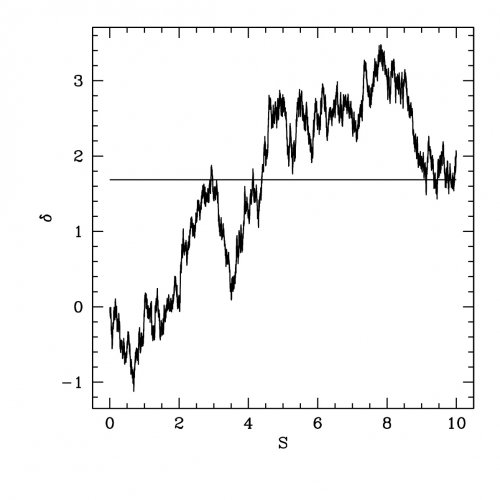
Figure 2: Markovian random walk of the density perturbation as function of the variance of the underlying random density field filtered at different scales. Click on the image to enlarge it Richard Bond, Shaun Cole, George Efstathiou and Nick Kaiser introduced the stochastic model of halo formation, also known as excursion set theory, in the early 90. In the original formulation, the derivation of an analytical formula for the halo mass distribution is limited to few ideal cases for which there is no physically meaningful definition of the halo mass. In a realistic case, the mass definition has to be consistent with that inferred from observations, however the stochastic equations of the model cannot be solved analytically, but only through time consuming numerical Monte Carlo simulations. This is because the way the mass is defined alter the filtering process of the density field such that the pseudo-time evolution of the random walks is no longer independent of their past history. Their evolution as function of the filtering scale becomes correlated. It is like having a stock whose price smoothly changes over time (instead of discontinuous jumps) because all investors buy and sell according to a pre-arranged set of past prices. To overcome this limitation the researchers have used a path-integral formulation of the halo random trajectories. The path-integral is a mathematical technique that allows the computation of transitional probabilities by summing up over all possible paths of a random process. Developed in the context of quantum mechanics by Richard Feynman, such methodology has analogs in statistical mechanics and is applicable to stochastic systems. Recently, Michele Maggiore at the University of Geneva and Antonio Riotto at CERN have been able to formulate the excursion set theory in terms of path-integrals. They have shown that in such formulation one can solve analytically the halo mass function for mass definitions that are consistent with observational estimates of halo masses.
It is within this mathematical framework that LUTH’s theorists have performed their calculation. However, to improve the theoretical modeling of the halo mass distribution they had to consider a further element. In the excursion set theory the density threshold reached by the random walks that form dark matter halos is inferred from a simplified model of the non-linear gravitational collapse of matter. Initial density fluctuations on very large scales tend to collapse approximately as isolated systems. Thus the gravitational infall is similar to that of a homogeneous sphere of matter. This is not the case at smaller scales, where distortions due to the shear of the velocity field associated to matter density fluctuations and other environmental effects make the collapse more anisotropic, approximately like that of a homogeneous ellipsoid. Because of this the collapse conditions change over different scales and randomly. On average the collapse follows at large scales that of a spherical object, while at small scales that of an ellipsoidal one. The astronomers have therefore implemented the excursion set theory in its path-integral formulation with a stochastic model of the halo collapse condition that mimic these peculiar features. The result of this computation is a mathematical formula of the halo mass distribution which manifestly depends on physical parameters that encodes the main features of the halo collapse. These parameters provide a physical explanation for the shape of this function over the all range of masses probed by numerical simulations. Even more important is the fact that the derived formula matches the halo mass distribution measured in N-body simulations with unprecedented accuracy (Figure 3).

According to the two researchers this study is only the beginning of a new approach to a complete theoretical description of the mass function of dark matter halos. Their work suggests several new directions of investigation. On the one hand, it will be interesting to extend the mathematical description to scenarios in which the initial density field obeys a non-Gaussian statistics, such as in high-energy physics and string theory inspired models of Inflation, the quantum mechanical process which is believed to have generated the primordial spectrum of density fluctuations. This will allow probing the physics of the very early Universe directly from upcoming measurements of the cosmic abundance of galaxy clusters. Another aspect that is worth further investigation is the stochastic modeling of the halo collapse condition. This can be improved to account for the precise cosmological dependence of the stochastic model parameters. A work that LUTH’s cosmologists intend to carry out in the near future.
[1] P.S. Corasaniti and I. Achitouv, Phys. Rev. Lett. 106 (2011) 241302 [2] P.S. Corasaniti and I. Achitouv, Phys. Rev. D in press.
Last update on 21 December 2021